筆者のところにはさまざまな原稿依頼が舞い込むのだが、今回の依頼主の団体名「日本建築美術工芸協会」を見て、不覚にもあぁこれは書きやすい、楽そうな原稿依頼だろうなと思ってしまった。なにしろ天文学は一般の方々のイメージでは科学というよりも、どちらかといえば芸術に近い。新聞やテレビを賑わせる天文・宇宙関係のニュースには必ずと言ってよいほど美しい画像や映像が添えられている。最先端望遠鏡で撮影されたさまざまな天体の色ととりどりの姿は、まるで前衛芸術かと見紛うほどのもの多い。最近では天体写真集が、科学を扱う出版社ではなく、技術や写真芸術を扱う出版社から出されたりするし、そうした宇宙の画像を中心とした展示会も、科学館ではなく、美術館で開催されることも多くなった。実際、筆者が監修している写真展「138億光年宇宙の旅ー驚異の美しさで迫る宇宙観測のフロンティア」は2023年の夏には広島の呉市美術館、冬には愛知県の岡崎市美術博物館で開催されたほどだ。
ところが、である。原稿依頼書を読み進むにつれ、その思い込みは見事に砕かれた。「第1回のテーマは「共鳴」といたしました」とあったからだ。これにはとても驚いた。共鳴という言葉そのものが、それほど一般的でない上、天文学の中での共鳴現象はきわめて取り扱いが難しく、同時になかなか理解しにくいものだからだ。 確かに、建築に携わる人にとっては共鳴(場合によっては共振)は免震構造など重要なメカニズムとして扱わなくてはいけないものなのだろう。しかし、美術工芸という観点ではあまり一般的ではないような気もする。一体、何を求められているのだろうか、お引き受けすべきかどうかと悩んでいるうちに一週間ほど時間が過ぎてしまった。えいや、と「ご依頼、光栄ですが、なにせ建築美術工芸には疎く、どうしてよいか悩んでいるうちに一週間過ぎてしまいました。天文学では「共鳴」はきわめて大事な現象なのですが、その解説で許してもらえるなら、お引き受けいたします」とお返事をした次第である。本稿が編集側の趣旨である「テーマを「共鳴」としたのは、違うアプローチをする方が「共鳴」することで化学反応が起こり、より良い協創ができる」という目的にどこまで合致できるかどうか、わからないが、いずれにしろ、宇宙における共鳴のいくつかを紹介することとしたい。
共鳴という現象で筆者がいつも持ちだす身近な例がブランコである。釈迦に説法かもしれないが大事なので解説しておこう。ブランコは振り子と同じく、紐(チェーン)の長さで揺れの周期、つまり振動数が決まる。この振動数を固有振動数と呼ぶ。固有振動数に近い振動数で、ブランコを周期的に押してやると、その押す力が弱くてもブランコの振幅はどんどん大きくなっていく。子どもが自然にブランコの上で、固有振動数に近い形で重心移動することで振幅を大きくさせるのも、この原理である。
宇宙では天体同士の軌道で同じ事が起きる。天体は決して接触するわけではないが、遠隔力である重力が効くため、共鳴するのだ。軌道の場合、その軌道周期が固有振動数の逆数、つまり、この軌道の周期がちょうど整数比となるところで共鳴が起きる。その代表例が木星のガリレオ衛星群だろう。木星を望遠鏡で覗いたときに、その傍に見られる衛星で内側からイオ、エウロパ、ガニメデ、カリストと並んでいる。前者三つの公転軌道周期は約1.8日、3.6日、7.2日であり、周期の比が1:2:4 となっている。木星に近いため、その重力の影響が強く、こうした共鳴状態に陥ってしまい、そのまま安定しているといえる。
一方、こうした共鳴が強いと逆に不安定になる場合もある。複数の天体が軌道共鳴の状態にある場合、大きな天体の重力の影響が勝り、小さな天体の軌道が大きく変化させられて、最終的にははじき出されるケースがあるのだ。安定、不安定のどちらも起こっているのが小惑星帯である。ここには100万を超える小さな岩石質天体、小惑星が存在しているが、木星の強大な重力によって、木星との軌道周期比が2:3、3:4、および1:1の場所にはヒルダ群、チューレ群、トロヤ群と呼ばれる小惑星の群れが安定して存在し、逆に3:1、5:2、7:3、2:1の場所には、小惑星がほとんど存在していない。これらの空白領域(空隙)は発見者の名前からカークウッド・ギャップと呼ばれている。
こうした共鳴現象がみごとに可視化されているのが、土星の環(リング)であろう。環は無数の主に小さな氷粒子でできていて土星の本体を公転している。つまり氷粒子は、それぞれが天体として軌道周期を持つ。一方、土星にはすでに100個近い衛星が見つかっており、そのうち土星に近い衛星のいくつかは、お互いに共鳴状態にあるペアがある上に、それぞれが大きな天体として、土星の環の粒子に軌道共鳴を通して影響を与えている。衛星との公転周期の比率で整数比のところがギャップになっているのだ。例えば、環の中で最も大きいカッシーニの空隙は、土星の衛星ミマスとの公転周期比が2:1となっている場所である。これ以外に様々な衛星によって、無数の共鳴があるため、土星の環はこれだけ見事な造形を生み出しているのである(下図)。
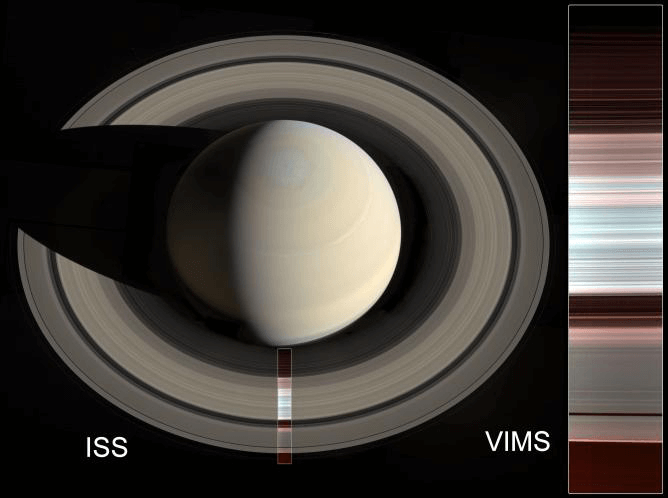
衛星の軌道共鳴によって細かなリング構造ができている。
最も大きな環の隙間がカッシーニの空隙。衛星ミマスと2:1の軌道共鳴の場所である。
右の図は、環の一部の赤外線画像で白から青色は主に氷粒子、赤色は鉱物質の砂粒粒子が多いことを示している。
©NASA/JPL-Caltech/Space Science Institute/G. Ugarkovic (ISS), NASA/JPL-Caltech/University of Arizona/CNRS/LPG-Nantes (VIMS)
一方、もっと身近に見上げる夜空にも共鳴の例がある。都会からでも見える月だ。月は満月でも半月でも同じ面、つまり兎が餅をつく模様がある表側を地球に向けている。これは月が地球をまわる軌道の周期(公転周期)と自らの天体がぐるっと回る周期(自転周期)とが一致しているからだ。この公転と自転の同期は潮汐ロックとも呼ばれるが、自転と公転が1:1の共鳴状態といえる。太陽系ではほかに太陽に最も近い水星のケースでは、自転と公転が3:2の共鳴状態だ。地球ー月系に比べ、軌道が円のひしゃげ具合や太陽からの距離で共鳴の度合いが弱く、1:1まで達せずに、3:2で落ち着いてしまったようだ。水星の軌道がもっと太陽に近く、円軌道なら1:1となっていたかもしれない。実は太陽系以外の恒星のまわりにも、たくさんの惑星系が見つかっているが、そのなかには中心の恒星にあまりに近いため、公転周期と自転周期が1:1となっていると考えられる例がたくさん見つかってきている。 こうなると、昼と夜が繰り返さず、昼半球と夜半球に二分され、恒星を向いた昼面では灼熱に、恒星の光が差さない夜面では極寒になる。地球のように大気があるとすこし和らぐのだが、そんな惑星に知的生命がいたら、暦や時間の感覚が我々とは全く異なることになるにちがいない。
ところで、自転と公転が共鳴状態にある地球ー月系では、次第に月が地球から遠ざかり、同時に地球の自転速度が遅くなっている。もともと月が生まれた46億年前頃には地球は数時間で自転し、月も現在の10分の1ほどの距離にあったとされている。さぞや迫力のあるお月見だったに違いない。それでは、将来はというと、月はどんどん遠ざかり、地球の自転もどんどん遅くなる。ある計算では、月の公転周期が現在よりも1.5倍ほどの場所まで遠ざかると、地球の自転周期も45日ほどになり、地球と月の自転周期、そして月の公転周期がすべて同じになる。筆者は、ひそかにこの状態を自転の完全共鳴と読んでいる。なお、この完全共鳴になるのは約60億年後なので、われわれ人類はこれを眺めることはできない。太陽の寿命が尽きて、地球は生命の住める環境ではなくなってしまうからだ。しかし、広い宇宙のどこかには完全共鳴状態の惑星衛星系に住む知的生命も存在し、大空の一点にとどまり、そこで満ち欠けを繰り返す衛星を眺めているのだろう。そこではどんな文化が育っているのか、知りたいものである。
1960年福島県生まれ。東京大学大学院、東京大学東京天文台を経て、現在、自然科学研究機構国立天文台上席教授、総合研究大学院大学教授。国際天文学連合副会長。理学博士。流星、彗星など太陽系天体の研究の傍ら、最新の天文学の成果を講演、執筆、メディア出演などを通して易しく伝えるなど、幅広く活躍。国際天文学連合では、惑星定義委員として準惑星という新しいカテゴリーを誕生させ、冥王星をその座に据えた。主な著書に「賢治と「星」を見る」(NHK)出版)、「面白いほど宇宙がわかる15の言の葉」(小学館101新書)、「新しい太陽系」(新潮新書)、「ガリレオがひらいた宇宙のとびら」(旬報社)、「星空からはじまる天文学入門」(化学同人)など。